Rotational Symmetry
Rotational symmetry has never been more fun!
Students build deep conceptual understanding by creating their own colourful mandala.
Suitable for: Senior Years
Skills: Geometry
Click here to get creative with Rotational Symmetry!
Learning Objectives
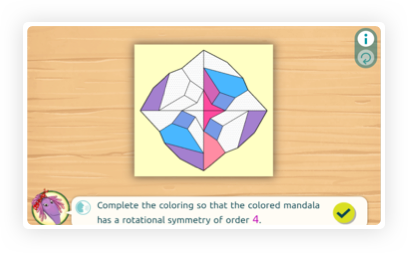
Colour a shape in a rotationally symmetrical way, with a specified order of symmetry.
Mathematical Background
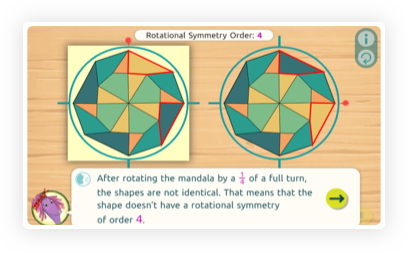
In geometry, transformations are rules that move points on the plane. Students learn about three special kinds of transformations - translation, rotations, and reflections - that preserve the relationships between the points on any shape they are applied to. A shape has symmetry if it looks the same overall after a transformation is applied. It has rotational symmetry if it looks the same after a rotation. The order of rotational symmetry tells us how many times this happens throughout a full turn. If it looks the same after half a turn (but not before), it has order 2; if it looks the same after a third of a turn, it has order 3, and so on.
Pay Attention to
- Active learning: The learner is engaged in a creative, hands-on process - they are encouraged to experiment, and the choices they make are meaningful.

- Teachable moments: The learner's actions are contextualised within more formal mathematical language as they go. This context does not present a barrier to student interaction; instead, it helps crystallise the underlying mathematical ideas they have already used in the activity.

- Immediate feedback: Matific quickly detects students who need guidance, providing low-stakes, targeted assistance to help them address any mistakes they make.